Overview
For my final project in Advanced Algorithms, I explored the question:
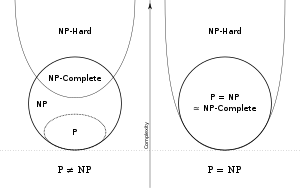
how was Boolean satisfiability (SAT) first proved to be NP-Complete?
While many NP-Completeness proofs rely on reduction from another NP-Complete problem, SAT was the
original. My research focused on understanding the Cook–Levin theorem, which
established SAT as NP-Complete and laid the foundation for computational complexity theory.
My Contributions
I focused on making the theorem accessible to myself and my peers. I:
- Researched the history and structure of the Cook–Levin theorem
- Clarified why SAT was chosen as the first NP-Complete problem
- Created a written report explaining the theorem step-by-step
- Developed a slide presentation summarizing the proof at a high level
Outcome
This project gave me a much deeper understanding of complexity theory
and the mechanics of NP-Completeness proofs. My write-up and presentation both served as
teaching tools for my classmates, making a dense and abstract topic more approachable.